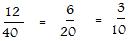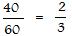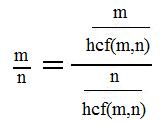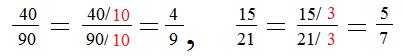Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Computer Programs for this Chapter
Return to index of all chapters in this volume
Volume B Chapter 1
Natural Numbers
Note: statements with an carot (^) will be generalized in later sections to apply to larger systems of numbers.
Click here to get a very intuitive introduction to the natural numbers and the addition operation on them.
Section 1 Basic ideas
What are natural numbers? One answer is that they are used for counting objects. This fact will be exploited in this section. But they were used in the previous volume, but not discussed in detail. A name N was given to the collection of all natural numers. Even a list of some numbers was given N = {1,2,3,...}. But 4, 5, 6, ... are natural numbers not shown in that list. It is obvious that no list of all natural numbers can be written. (The "Brute force" method of listing every number does not work here!). Instead, some other method must be used. From the process of counting, the following relationships between pairs of adjacent numbers are observed:
2 is the immediate successor of 1, 3 is the immediate successor of 2, 4 is the immediate successor of 3, ....
This should be an infinite list of successor statements. But all of these statements are components of the single open statement:
(*) x+1 is the immediate successor of x
This is one of the fundamental properties of N. (It is possible to assemble some axioms to determine all natural numbers. One of the Peano postulates defines the immediate successors of all natural numbers without using the operation of addition. But this approach to N is not done here.)
(*) is acepted as a fundamental property of natural numbers. As an immediate result, there cannot be last or biggest natural number. Its successor would be even bigger.
But (*) alone does not guarantee the existence of natural numbers. It simply guarantees the existence of successors if numbers exist. The infinite sequence
4.9, 5.9, 6.9, 7.9, 8.9, 9.9, 10.9, 11.9, 12.9, ...
where each number n+.9 has a successor n+1+.9. Yet this is not the set N of all natural numbers, because 1 is not in it.
After asserting the existence of the number 1 in N, then immediate successors cause a chain reaction of making all natural natural numbers exist in N. The following is a working definition.
[1.1] (Inductive definition of N) The content of the set N of all natural numbers has the following properties
(a) 1 is in N. However, it is not the immediate successor of anything in N.
(b) For any number in N there is an immediate successor in N. (It is different from all previous natural numbers.)
Notation: (b) if n is in N then n+1 is in N.
Notice that an effort is being made to define the set N, and not define what each natural number is, but how it relates to another number, namely through being successors. Because part (b) is infinitely repetitive, there is no last natural number. However, there is a first natural number, namely 1 because of part (a). Notice that zero is not a number in N according to [1.1]. (It will be "attached" later to make the set of non-negative integers.)
[1.2] (Principle of Linear Order*) For any pair of unequal natural numbers, a number must be less than the other. Also true is the fact that the other number must be the greater in the pair.
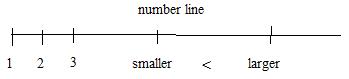 This principle allows the natural numbers to be assigned to consecutive points (markers) on a horizontal straight line, starting with 1 and going to the right. By this assignment a smaller number is located to the left of a larger number. A larger number is located to the right of a smaller number. But those readers who are familiar with complex numbers have seen a system in which some numbers cannot be compared for size: it cannot be said which of the numbers 3 + 4i and 4 + 3i is larger than the other. The points for all complex numbers is a plane, not a line. The complex numbers are not linearly ordered. Complex numbers form a number system that discussed in chapter 5 in this same volume of number systems.
This principle allows the natural numbers to be assigned to consecutive points (markers) on a horizontal straight line, starting with 1 and going to the right. By this assignment a smaller number is located to the left of a larger number. A larger number is located to the right of a smaller number. But those readers who are familiar with complex numbers have seen a system in which some numbers cannot be compared for size: it cannot be said which of the numbers 3 + 4i and 4 + 3i is larger than the other. The points for all complex numbers is a plane, not a line. The complex numbers are not linearly ordered. Complex numbers form a number system that discussed in chapter 5 in this same volume of number systems.
From continual use of natural numbers a person is aware that they are different from fractions and decimal numbers, at least in appearance. But they are different in nature. It is meaningful to say that the number 5 is next to the number 4. But it is not meaningful to say that the fraction 3/8 is next to the fraction 2/8 because there are many other fractions between them, including the fraction 5/16. Between any two fractions is another fraction, their average (midpoint on the number line). The same is also true for real decimal numbers.
***
Subsets of natural numbers may or may not include all of them. Each of the following is a subset containing some natural numbers:
{25,14,19,8,21,11,26}
{18, 24,17,5,8,12}
{20,13,4,19,11,28,7}
A simple examination of each list reveals a smallest number in it. Even an infinite list like
{100,200,300,400,...} (all the numbers with two zero digits at the end)
still has a smallest natural number in it. It is impossible to create any non-empty list of natural numbers, finite or infinite, without a smallest number in it. This property of the natural numbers also distinguishes them from fractions and decimal numbers. The infinite list of fractions continually getting smaller:
{1/2, 1/3, 1/4, 1/5, 1/6, ...}
has no smallest fraction.
[1.3] (Well Ordering Principle of N)
Every non-empty subset of natural numbers has a smallest natural number in it.
Even infinite subsets have a smallest natural number in it. The set 2N = {2,4,6,8,10,12,...} of all even natural numbers also has a smallest natural number in it, namely 2.
***
The original use of the natural numbers was for counting. Intuitively speaking, to count objects in some collection, the natural numbers in their increasing order are associated ("attached") one-on-one to the objects. It is convenient, but not necessary, if all of the objects are arranged in a horizontal row.
[1.4] (Counting by Association)
To count the number of objects in a collection, associate with each object in the collection a single distinct natural number, starting with 1 and continuing to the right (getting immediate successors) one number at a time, so that every object in the collection has a single natural number from
Nn = {1,2,3, ... , n-1,n}
associated with it. The collection is said to have (exactly) n objects if n is associated with the last object. The collection with n objects and no more is said to be finite. But if the counting process never stops then all the natural numbers in N will be involved, and the collection is said to be infinite.
To make the counting process of objects accurate, certain rules must be followed:
(a) No object should be counted twice. (Different natural numbers cannot be associated with the same object).
(b) Different objects cannot be associated with the same natural number.
These rules determine a one-to-one correspondence between natural numbers and objects. (One-to-one correspondences will be discussed in a later volume.)
Each of the finite subsets Nn has a number n indicating the number of natural numbers are in that list. Some people like to have the symbol ω (the last letter in the Greek alphabet) to indicate the number of natural numbers in the set N of all natural numbers. ω is the first transfinite or infinite number introduced in these discussions. Nω = N. Sets with a transfinite number of objects produce some interesting arithmetic peculiarities that go against intuition developed by daily use of the common natural numbers. More discussions of these strange new numbers can be found in a section on one-to-one correspondences in the chapter on relations.
***
There is a physical model for the addition of two natural numers, called addends. Problems caused by physical extremes are ignored, such as huge numbers, sizes, weights, space... .
[1.5] (Working method of addition of natural numbers*) To add natural numers m and n together count out m balls and put them in a first bag. Count out n balls and put them in second bag. Have a third empty bag ready. Pour the content of the first bag into a third bag, and then pour the second bag into the third bag. This process can be denoted by the symbols
content of the first bag + content of the second bag = content of the third bag
Count all the objects in the third bag to get the sum m + n.
Using induction it is possible to obtain a non-physical definition of addition. However, some essential properties of addition can be seen from [1.5] (and logically deduced from that non-physical definition.). The first property is that there are enough natural numbers to perform any addition operation on those numbers.
[1.6] (Closure of the addition operation*) For any two natural numbers there will always exist a third natural number that is equal to their sum.
Notation: For natural numbers m,n, m + n can always be computed to produce a natural number.
Theoretically, it is always possible to pour the contents of the two bags into a third bag and then count the balls in the third bag.
Following the rules of English grammar, the addition operation must be written from left to right. The following says that this order is not important.
[1.7] (The commutative law*) The two sums are the same for any pair of numbers that are added in either order
Notation: For any pair of numbers m,n, m + n = n + m.
Content of the first bag + content of the second bag and content of the second bag + content of the first bag pour the same number of balls into the third bag. No balls are lost and no extraneous balls are added to the first two bags by the change in order of pouring.
A formal proof of [1.7] involves a careful use mathematical induction and is beyond the scope of any discussion in these volumes.
There are other systems in which a form of addition has been defined. It is customary to consider all additive systems to be commutative. (Multiplicative systems may or may not be commutative.)
It is possible to combine three bags of balls into a single fourth bag. (Parentheses around the combining of bags means that combining is done before any other combining.) Keeping the bags in order, there are two ways of combining the contents:
Method 1 (first + sign acts before the second + sign): (content of first bag + content of second bag) + content of third bag
Method 2 (second + sign acts before the first + sign): content of first bag + (content of second bag + content of third bag)
Since no balls are lost and no extraneous balls are added by either method, the the content of the fourth bag is the same for either method.
Example: find sum 3 + 4 + 5.
Method 1: (3 + 4) + 5 = 7 + 5 = 12.
Method 2: 3 + (4 + 5) = 3 + 9 = 12.
Notice that the order 3,4,5 is the same in both methods and there are exactly two additions for each method.
[1.8] (The associative law*) The sum of three natural numbers is the same no matter which of the two additions is done first.
Notation: For any three natural numbers k, m, n, (k + m) + n = k + (m + n).
A formal proof of the associative law involves multiple use of mathematical induction.
Using both laws [1.7] and [1.8] it can be said that numbers and addition operations can be added in any order. This fact guarantees that the total cost of all items bought in a store will be the same, no matter in what order the items are selected for adding up the prices at checkout.
***
Using only natural numbers, addition of them produces larger numbers, because the whole is greater than any of of its parts. (On the number line the sum is found always to the right of every number in that sum.) The following is an obvious but useful property of natural numbers.
[1.9] (Sum is larger) The sum of two or more natural numbers is larger than any of those natural numbers. (Equivalently, any natural number in a sum is smaller than that sum.)
Notation: k + m + n > k, k + m + n >m, k + m + n > n
The definitions [1.10a] and [1.10b] below shift the burden of defining inequalities from positions in the set of all natural numbers to the operation of addition. They both are restatements of [1.9]. They look at the same situation as [1.9] but in different ways.
A natural number n is less than a natural number s if and only if n is part of a sum equal to s.
[1.10a] (Less than*) A natural number n is less than a natural number s if and only if s = n + x, where x is some natural number.
Notation: n < s
[1.10b] (Greater than*) A natural number s is greater than a natural number n if and only if s = n + x, where x is some natural number.
Notation: s > n
From the wording "less than" and "greater than" are dual ideas. And it is not difficult to show that n < s and s > n are equivalent (open) statements.
5 < 12 because there is a solution to the equation 5 + x = 12 using a natural number, namely 7.
But it is impossible to solve the equation 9 + x = 6, using only natural numbers. The sum 9 + x becomes too big (larger than 9) when x is replaced by any natural number. This impossibility means that the statement 9 < 6 is false.
[1.11a] (Telescoping inequalities^)
If one natural number is less than the second, and the second natural number is less than the third, then the first natural number is lless than the third.
Notation: for any natural numbers k,m,n, if k < m and m < n then k < n.
[1.11b] (Telescope^)
If one natural number is greater than the second, and the second natural number is greater than the third, then the first natural number is lgreater than the third.
Notation: for any natural numbers k,m,n, if k > m and m > n then k > n.
An intuitive argument for [1.11a] is the following:
In the horizontal list [1.1] of natural numbers in increasing order,
if a is to the left of b, and b is to the left of c then a is to the left of both b and c
This supports the truth of [1.11a]. A similar statement may be made about [1.11b] using "right" in place of "left". (a result of the duality of < and >), replacing the words "left" and "less" by "right" and "greater."
A more formal argument for [1.11a] is the following:
Let a,b,c be natural numbers such that a<b and b<c. Then a is a part of whole b, so
(#)
b = a + some natural number
Similarly:
(##)
c = b + some natural number
Replace the b in equation (##) by the right side of the equation in (#) to get:
c = a + some natural number + some natural number
The two unimportant natural numbers can be added. This means that a is part of the whole c. Therefore, a<c.
[1.12a] (Addition of inequalities <*)
For any natural numbers a,b,c,d,
if a<b and c<d
then
a+c<b+d.
[1.12b] (Addition of inequalities >*)
For any natural numbers a,b,c,d,
if a>b and c>d
then
a+c>b+d.
For proofs of these two statements click here. They can be extended to involve more variables.
***
Subtraction is another operation on the natural numbers, but it is limited because 0 and negative intergers are not natural numbers. It is defined using an equation that involves addition of natural numbers.
[1.13] (Subtraction*) The difference m - n of two natural numbers m and n is that unique natural number x (if it exists) that satisfies the equation m = n + x.
The parenthetical expression (if it exists) means that [1.13] does not guarantee a solution. 10 + x = 7 has no natural number solution for x (a sum of two natural numbers is larger than either natural number, and the sum 7 is smaller than the addend 10). Therefore the subtraction 7 - 10 cannot be done usiing only natural numbers.
For any pair of distinct natural numbers by [1.2] one must be the larger and the other must be the smaller. Therefore, a limited subtraction is always possible by subtracting the smaller from the larger (larger - smaller). If m and n denote arbitrary but unequal natural numbers, no information is given about which is larger. The subtraction m - n may not be possible because n is the larger. The following is a solution to this problem and makes limited subtraction always possible for distinct natural numbers - simply make sure that the smaller number is subtracted from the larger:
[1.14] (Absolute value of the difference of two unequal natural numbers)
|m - n| = m - n if m is the larger; |m - n| = n - m if n is the larger.
Examples: |5 - 3| = 2, |6 - 9| = 9 - 6 = 3, |100 - 40| = 60, |40 - 100| = 60.
Intuitively speaking, absolute value avoids the use of negative numbers. It is widely accepted that distance is not negative. If m and n locate distinct markers on the number line, then |m - n| is the distance between them. (See the discussion just after [1.2].)
Section 2 Multiplication of Natural Numbers
In the previous section it was mentioned that the natural numbers can be used to count objects: 3 apples means apple, apple, apple. A natural number can also be used to count numbers: 3 4's means 4, 4, 4 . It is easy to find the sum 4 + 4 + 4. Into an empty bag, add 4 objects, then add 4 more objects, and finally add 4 more objects. Exactly 3 times the addition of objects to the bag was made. Count the total number of objects in the bag. 12 of course. Found was the product 3x4.
[2.1] (Algebraic method for evaluating a product*)
The product nw of a natural number n and a numerical or algebraic quantity w is equal to the sum of that quantity w repeated n times in the addition process.
Integer n is called a coefficient of w. Integer n may also be called a replicating factor. when it indicates repeated addition.
Notation: nw = w + w + ... + w [n w's appear in the indicated sum]
A logical definition of multiplication involves mathematical induction. (Click here to see a definition involving induction. Integer n is called a coefficient of w.
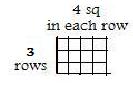 Finding areas of rectangles by multiplying lengths of adjacent sides suggests a more organized method for evaluating a product of natural numbers. Let the objects being counted small squares. Instead of using repeated addition (linear form) sq sq sq sq + sq sq sq sq + sq sq sq sq and then counting the sq's, use a two-dimensional rectangular form wiith rows of 4 squares under each other, as shown in the adjacent figure, and then count the squares. This suggests that areas of geometric rectangles provide a method to calculate the product of two natural numbers.
Finding areas of rectangles by multiplying lengths of adjacent sides suggests a more organized method for evaluating a product of natural numbers. Let the objects being counted small squares. Instead of using repeated addition (linear form) sq sq sq sq + sq sq sq sq + sq sq sq sq and then counting the sq's, use a two-dimensional rectangular form wiith rows of 4 squares under each other, as shown in the adjacent figure, and then count the squares. This suggests that areas of geometric rectangles provide a method to calculate the product of two natural numbers.
(Geometric method for evaluating a product)
To find the product nm of a natural number n and a natural number m, construct a rectangle with height n and width m. Then count the number of squares (square areas) the rectangle contains.
In addition to the above methods for evaluating a product, an inductive definition can be found by clicking here. However it is advisible to wait until section 3 of this chapter.
[2.2] (Commutative law for multiplication of natural numbers*)
For any natural numbers n and m, nm = mn.
(Dual: for addition: n + m = m + n)
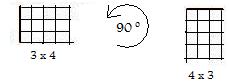 Mathematical induction can be used to prove this law for natural numbers. However, a simple geometric argument supports it. Draw the rectangle with height m and width n. Then there are mn squares inside the rectangle. Rotate the triangle through 90° Now it is a nm rectangle. The number of squares is the same because the two rectangles are congruent. The figure to the right shows this argument for the product 3x4 = 4x3.
Mathematical induction can be used to prove this law for natural numbers. However, a simple geometric argument supports it. Draw the rectangle with height m and width n. Then there are mn squares inside the rectangle. Rotate the triangle through 90° Now it is a nm rectangle. The number of squares is the same because the two rectangles are congruent. The figure to the right shows this argument for the product 3x4 = 4x3.
[2.3] (Associative law for multiplication of natural numbers*)
For any natural numbers k,m,n, k(mn) = (km)n.
(Dual: for addition: k + (m + n) = (k + m) + n)
Again this law can be proven using mathematical induction. A geometric argument supports it, using a rectangular three dimensional box containing unit cubes whose count = volume. It will not be given here, and the associative law is assumed to be true.
The definition [2.1b] connects multiplication with addition through counting. Since 3 objects plus 2 objects equals 5 objects, it is reasonable that 3w + 2w = 5w, where w is a natural number. (Actually, w may be any numerical or algebraic expression.) So (3 + 2)w = 3w + 2w. A generalization of this idea supports the following:
[2.4a] (Right distributive law*)
For any natural numbers m,n,w, (m + n)w = mw + nw.
If there are m objects and n more objects are added then there are a total of (m + n) objects. Consider the number w as an object (perhaps written on a piece of paper). Then mw + nw = (m + n)w.
This time consideer an expression (u + v) appearing in a sum 3 times: (u + v) + (u + v) + (u + v). By definition [2.1b] this sum can be written 3(u + v). But removing the parentheses and using the commutative and associative laws this repeated sum is equal to 3u + 3v. Therefore 3(u + v) = 3u + 3v. A generalization of this idea supports the following:
[2.4b] (Left distributive law for natural numbers*)
For any natural numbers u,v,n, n(u + v) = nu + nv.
Actually, the commutative law makes these two distributive laws logically equivalent. The w in [2.4a] can be repositioned in front of the sum (m + n) and become a coefficient. In some later systems neither distributive can be proven directly from the other using a commutive law.
The number 1 is the smallest natural number. But it also as a special role in multiplication;
[2.5] (Multiplicative identity*) For any natural number n, the product: 1n = n.
In [2.1b] multiplication was introduced as repeated addition. It is possible to have a number repeatedly multiplied by itself. 52=5x5 = 25, 103=1000, w2 = ww, w3 = www.
[2.6] (Powers^)
The n-th power wn of any quantity w is equal to the product of that quantity repeated n times in the multiplication process: wn = ww...w where w appears in the multiplication process n times. The integer n is called an exponent on w.
[2.7] (1 As exponent*) w1 = w.
So [2.7] and [2.5] continue the duality between exponents and coefficients.
[2.8] (Associative law for multiplication*) For any natural numbers u(vw) = (uv)w.
(Duality: for addition: u + (v + w) = (u + v) + w.)
[2.9] (Exponential law*)
(uv)n = unvn
This law is the dual of the distributive law [2.4b]. The supporting argument is similar.
[2.10] (Comparison laws*)
(a) if u < v then nu < nv
(b) if u > v then nu > nv
The proof of (a) is simple. If u < v then there is a natural number x such that v = u + x. Multiply both sides of this equation by n to get nv = nu + nx. Since nx is a natural number nu < nv. The same argument can be made for part (b).
[2.11] (Cancellation law*)
nu = nv implies u = v
The argument for this law directly supports the contrapositive: if u is not equal to v, then nu is not equal to nv.
If u is not equal to v, then by [1.2] (Law of linearity) u < v or u > v. If u < v then nu < nv by [2.10a], which means that nu is not equal to nv. Similarly if u > v then nu > nv by [2.10b], which also means that nu is not equal to nv.
Since n is a natural number then it cannot be zero. In the next section about integers, this condition n not equal to zero will be explicitly stated. An argument supporting [2.11] will be supplied there.
The use of the commutative law can be used to prove that [b] follows immediately from [a].
Addition and multiplication combine two numbers to produce a sum and product respectively. They are called binary operations. A binary operation combines any two things from a collection and produces a single quantity that is in that same collection (closure). The commutative and associative laws can be stated as
u o v = v o u
[commutative law]
u o (v o w) = (u o v) o w
[associative law]
where o may be replaced by either the addition or multiplication symbol. In most systems that the reader may encounter, the associative law will hold true. But in some systems the commutative law may not hold true. Discussed later in this volume are systems of functions, and in other volumes matrices, and quaternions, all of which are not in general commutative. It is customary to write an operation that is not commutative as multiplication.
***
If a product is equal to the multiplication of two or more natural numbers, then each of those natural numbers is called a factor or divisor of the product. The natural numbers 3 and 4 are factors of 12 because 12 = 3x4. Another test of being a factor is to divide the number into the suspected product number. The number 3 divides into 12 completely producing 4. But the number 5 does not divide completely into 12. The number 2.4 is not a natural number. Intuitively speaking, the fraction 12/5 is not equal to any whole natural number. Instead of factor the term divisor is used. Therefore, 3 is a divisor of 12 because it divides completely into 12.
[2.12] (Factors and divisors^) A given first natural number is a divisor (or factor) of a second natural number if and only if the second number is equal to a product of natural numbers, one of which is the given first number.
Notation: k | n means that number k is a divisor (factor) of number n.
If k is a divisor of n then k is part of a product of numbers equal to n. This means that
n = kx
where x is an unknown natural number. Quite often it is not what number x equals, only that a number for x exists. For example, 5 | 30 because the eequation
5x = 30
obviously has a solution which is a natural number.
[2.13] (Test for divisor by division)
The natural number k is a divisor of a natural number n if the fraction n/k is equal to a (whole) natural number. If it is equal, then that natural number is equal to a divisor of n. (The two divisors may be equal.)
Logically, the statement [2.13] is out of place, because division has not yet been defined. But this premature use of fractions here makes the process of determining whether or not a natural number is a factor very simple and clear.
For a natural number to be a perfect square, the two factors, by definition, are equal. For example, 81 = 9x9. The fraction 81/9 = 9. Therefore, 9 is a dividor of 81 and 9 is the "other" divisor.
The division n/k can be done more conveniently by electronic devices, such as a calculator.
[2.14] (Multiples*)
A natural number m is a multiple of a natural number n iff n is a divisor of m.
For example,
{ 21,33,48,81,99}
is a list of some of the multiples of 3. The number 3 is a divisor of every number in the list. The number 3 itself could be included in the list.
A duality exists between divisor and multiple: 7 is a divisor of 21 21 is a multiple of 7.
Sometimes for a given natural number all of its divisors are wanted. These can be given in a list { }. One reliable but laborious way to get this list for a natural number n is to evaluate all of the fractions
n/1, n/2, ... n/m
to see which fractions equal (whole) natural numbers. The denominators come from all the natural numbers in Nn = {1,2,...,n}. For example, evaluations of
6/1, 6/2, 6/3, 6/4, 6/5, 6/6
show that {1,2,3,6} is the list of all the factors of the natural number 6.
For any natural number there is a (finite) list of all the natural numbers that are its divisors.
The list of all divisors of 12 is {1,2,3,4,6,12}
The list of all divisors of 40 is {1,2,4,5,8,20,40}
The list of all divisors of 48 is {1,2,3,4,6,8,12,24,48}
The list of all divisors of 17 is {1,17}
Click here to see some facts that reduce the number of fractions to be tested for complete division.
There may be much computation even after removal of some of the fractions because many fractions may remain to be tested for complete division. especially if the natural number is very large, such as 9473651. And done by hand or calculator it is easy to miss some of the divisors. Click here to find a computer program (#1) to produce this list of all the divisors of a natural number (within the capacity of the machine, often less than or equal to 4 294 967 291).
By [2.5] 1 is a divisor of every natural number. Also every natural number n is a divisor of itself. These two numbers, 1 and n must be in every list of all divisors. For any natural number n, the numbers 1 and n are called trivial divissors of n. Divisors not trivial are called non-trivial. In the above lists the non-trivial divisors are in darker boldface.
[2.15] (Primes*) A prime is a natural number that is larger than 1 and that has only trivial divisors. A number larger than 1 but not a prime is called composite.
The following is a list of all the primes that are less than 100..
(&) {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,57,59,61,67,71,73,79,83,89,97}
It is convenient to use a computer to show that the natural number 2,147,483,647 is a prime. In fact it is the largest positive prime in many computer systems of 32 bit words.
The ancient Greek geometer Euclid proved that the list of all primes is infinitely long. Another ancient Greek, Eratothenes, discovered a method, called a sieve, for finding all primes. Click here to see a discussion of this method. No algebraic formula has yet been invented for finding all the primes. It seems that the primes are distributed somewhat randomly among all the natural numbers.
The numbers 42 and 87 are composite. They are not in the list (&). For convenience later, 1 is not allowed to be a prime.
Intuitively speaking, a composite natural number may be "broken down" into smaller pieces, its divisors. The composite number 45 can be broken down into divisors 9 and 5. A prime cannot be broken down into smaller non-trivial pieces. The number 17 has only trivial divisors, and cannot be broken down into smaller non-trivial pieces.
Sometimes the divisors themselves can be broken down. 45 = 9 x 5 but 9 can be broken down into 3 and 3, so that
45 = 3 x 3 x 5.
None of these divisors can be broken down further. The number 45 has been broken down into primes and the "breaking down" process stops there. Using exponents,
45 = 32 x 5.
This process of breaking down factors into smaller factors to get prime factors is based on the following theorem:
[2.16] (Transitive property of being a divisor^)
If a first natural number is a divisor of a second natural number, and that second natural number is a divisor of a third natural number, then the first natural number is a divisor of the third.
For example, 3 is a divisor of 12, and 12 is a divisor of 84, so 3 is a divisor of 84. Click here to see a simple proof of this theorem.
The following is an immediate result of [2.16]
[2.17] (*)
If a natural number is not a divisor of a second natural number, then no multiple of the first number can be a divisor of the second number.
For example 2 is not a factor of 99, then 4,6,8,10,... cannot be factors of 99.
Non-trivial divisors of a given natural number are smaller than that number. Usually the smaller the number the easier it is to find its divisors, which in turn will be divisors of the original natural number. For example it is obvious that 10 is a divisor of 560. But 2 and 5 are divisors of 10. Therefore 2 and 5 are divisors of 560. Dividing 10 into 560 produces 56 which is a divisor of 560. Since 56 = 8x7, and 2 is a divisor of 8, the prime divisors of 56 are 2 and 7. Therefore the list of all prime fdivisors of 560 is {2,5,7}. This discussion shows a method for finding all the prime divisors of a natural number.
Every breaking down a natural number into prime divisors will produce the same prime divisors. (Click here for a computer program that lists all the prime factors of a natural number.) But 560 is not equal to the product of its prime divisors because there are composite divisors. For example 56. However 560 = 16x5x7 = 24x5x7. Click here for a brief discussion of complete factorization of any natural number.
***
Besides the collection N of all natural numbers, there are other collections of natural numbers, some of which are useful in reality and in later discussions. The list of all even natural numbers
2N = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, ...}
can be "constructed" is two ways. One way is to multiply all numbers in N by two:
2(1), 2(2), 2(3), 2(4), 2(5), 2(6), 2(7), 2(8), 2(9), 2(10),...
For this reason this collection of all even natural numbers may be given the name 2N. But each of the numbers in 2N contains 2 as a factor, so each number is a multiple of 2. Moreover, 2N contains all of the multiples of 2.
In general each number in the list N may be multiplied by any natural number k to produce a new list kN of all multiples of the number k:
kN = {1k, 2k, 3k, 4k, 5k, 6k, 7k, 8k, 9k, 10k,...}
The collections of all multiples of some integer often play important roles in later discussions in some of these volumes. One reason is the fact that the collection is closed under addition. This means that the sum of any two multiples of the same number is also a multiple of that number. The following is a fact that supports this statement:
[2.18] (Addition of numbers with a common divisor)
Any common divisor of two (or more) natural numbers is a divisor of their sum.
Notation: if k | m and k | n then k | (m+n).
Suppose k | m and k | n. Then there are natural numbers x,y that solve equations m = kx and n = ky . Now a form of the distributive law is kx + ky = k(x + y). Therefore,
m + n = kx + ky = k(x + y).
Since m + n = k(x + y) and (x + y) is a natural number, k | (m + n).
The list kN is closed under addition. A collection of numbers not closed under addition would be a defective system in many cases. For example, in the list {4,7} there are just two numbers. It is not closed under addition, because 4+7 = 11 and 11 is not in the list. In fact, the only collections of natural numbers, closed under addition, are all the multiples of some natural number. This fact will be discussed in the next section.
Suppose the coefficients in the collection kN become exponents:
k, k2, k3, k2, k4, k5, k6, k7, k8, k9, k10, ...
This is the list of powers of k. It is the dual of kN. No notation is given as name for the list of powers. Nk already has another meaning in mathematics.
In the collection of powers of some natural number, the product of any two natural number is back in the collection. So the colllection is closed under multiplication.
A collection of numbers not closed under multiplication would be a defective system in many cases. If only 4 and 7 were in some collection, then that collection of just two numbers is not closed under multiplication, because 4x7 = 28 and 28 is not in the collection. In fact, the only collections of natural numbers (having some natural number not 1), closed under multiplication, are all the powers of some natural number.
***
The following are three equivalent fractions:
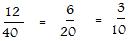
To get the second fraction, divide both the numerator 12 and denominator 40 of the first fraction by 2. To get the third fraction divide the numerator 6 and the denominator 20 of the second fraction by 2.
The following statements are copies from above:
The list of all divisors of 12 is {1,2,3,4,6,12}
The list of all divisors of 40 is {1,2,4,5,8,20,40}
The factor 2 is in both lists. The factor 4 is also in both lists. To get the third fraction directly from the first, divide both the numerator 12 and denominator 40 of the first fraction by 4.
A divisor is common to two or more sets of divisors if it is in all the sets. (It is in the intersection of the all the sets.)
A fraction retains the same value if both its numerator above and denominator below are divided by a common factor. Those two divisions produce natural numbers because the division involves factors.
The list of common divisors of 40 and 60 is {1,2,5,10,20}. The greatest common divisor is 20. Use it to divide both numerator 40 and denominator 60 of the first fraction to get the second fraction:
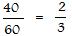
The reader can make the lists of all factors of 40 and of 60, and verify that the natural number 20 is the largest factor in both lists.
[2.19] (Greatest common divisor*) The greatest common divisor (or highest common factor) of two natural numbers is the largest divisor that is in both lists of all factors.
Notation: gcd(m,n) = greatest common divisor of natural numbers m and n.
Other notation: gcd(m,n) is the greatest common divisor of natural numbers m and n.
A technical definition of gcd will be given later.
gcd(12,40) = 4.
From
The list of all divisors of 40 is {1,2,4,5,8,20,40}
The list of all divisors of 48 is {1,2,3,4,6,8,12,24,48}
(the common divisors are in boldface) it is seen that gcd(40,48) = 8.
The reader can verify: gcd(8,10) = 2, gcd(15,9) = 3, gcd(12,12) = 12, gcd(8,27) = 1.
Without the laborious work of finding and listing all factors, the following can be stated as true: gcd(28459,28459) = 28459, gcd(1,25943) = 1 gcd(10,20) = 10.
Click here for a computer program (#4) that will find among other things the highest common factor of two natural numbers.
It is easy to expand [2.15] to define the gcd of more than two natural numbers: gcd(4,6,26) = 2. In this situation, there are three lists, a list of all factors of 4, a list of all divisors of 6 and a list of all divisors of 26. The numbers 1 and 2 are in all three lists, but nothing larger than 2 is in all three lists.
1 is a factor of every natural number. It may happen that it is the only number in both lists of all factors of two natural numbers, such as 8 and 27: gcd(8,27) = 1.
the list of all divisors of 8 = {1,2,4,8};
the list of all divisors of 27 = {1,3,9,2 7}.
[2.20] (relatively prime*) Two natural numbers are relatively prime if and only if their greatest common divisor is 1.
Notation: natural numbers m and n are relatively prime if and only if gcd(m,n) = 1 .
A ratio of natural numbers is a form m/n where m is the numerator and n is the denominator. The ratio is in lowest terms if the numerator and denominator are relatively prime.
The greatest common divisor of two natural numbers is a divisor of both numbers. Therefore its division into each number produces two natural numbers. The following shows what happens from this division.
[2.21] (Lemma) If each of any pair of natural numbers is divided by their greatest common divisor then the resulting quotients are relatively prime natural numbers.
Notation: for any natural numbers m,n the quotients

are relatively prime natural numbers.
A proof of [2.21] will be given later.
Recall from elementary arithmetic a ratio is not changed if both numerator and denominator are divided by the same quantity. Therefore,
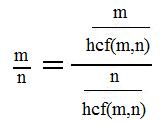
Example1: The ratios 60/70 and 15/25 are not in lowest terms because gcd(40,90) = 10 and gcd(15/21) = 3. Then dividing gcds into the numerators and denominators produces ratios that are in lowest terms:
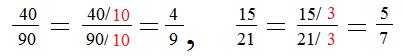 The number 5 is a common divisor of 40 and 90. Let the reader show that numerator = 40/5 divided by denominator = 90/5 produces a ratio not in lowest terms. Is it equal to ratio 40/90 ?
***
Although the definition [2.19] provides motivation for the name "greatest common divisor" the method there for computing gcd usually requires much computation especially for large numbers. The following provides a more efficient method.
The number 5 is a common divisor of 40 and 90. Let the reader show that numerator = 40/5 divided by denominator = 90/5 produces a ratio not in lowest terms. Is it equal to ratio 40/90 ?
***
Although the definition [2.19] provides motivation for the name "greatest common divisor" the method there for computing gcd usually requires much computation especially for large numbers. The following provides a more efficient method.
Given a pair of unequal natural numbers. By the linear ordering principle [1.2] one number must be the larger and the other is the smaller. Either the first or the second number could be the larger. In other words, the order is one of the following:
larger, smaller or smaller, larger
Form the difference larger - smaller. It is another natural number. Replace the larger of the pair of numbers by this difference:
larger - smaller, smaller or smaller, larger - smaller
In either case a new pair of natural numbers is produced.
It can be proven that the gcd of a pair of numbers is not changed when the larger is replaced by their difference. It can also be proven that repeating replacement process will eventually produce a pair of equal natural numbers. (Then the replacement process must stop.) Each of those equal numbers must be the gcd of the original given numbers.
Example:To find thegreatest common divisor of the pair 40,60.
hcf(40,60)
= hcf(40,60-40) 60 is the larger and is replaced by 60 - 40
= hcf(40,20)
= hcf(40-20,20) (40 is the larger and is replaced by 40 - 20
= hcf(20,20)
= 20
from equal numbers.
Click here for another example of finding the hcf.
Make a slight change at the beginning. If the given natural numbers are equal, then either number is the gcd. If they are unequal then proceed with the replacement process. The following is a complete and more formal description of the process. The variables m,n change values during the replacement process.
[2.22] (Subtraction algorithm for finding hcf*)
Given two natural numbers m,n. To find the hcf(m,n).
(a): if m=n, then then either m or n is the greeatest common divisor. Exit algorithm.
(b): if m > n then replace m by m - n. Go to (a).
(c): if n>m then replace n by n - m. Go to (a).
Click here for a computer program to execute the algorithm [2.22] and let the computer do the computation. But if the reader does the computation for hcf(1000,5) = 5 he will discover a type of inefficiency of [2.22]. Later another much more efficient alborithm will replace algorithm [2.22].
***
In [2.14] a multiple was defined: if u is a divisor of w, then w is a multiple of u. This reciprocal relationship is a duality between "divisor" and "multiple." For many of the facts about fdivisors there are dual facts about multiples. The dual statement of [2.16] can be obtained by replacing every appearance of "divisor" by the word "mulltiple" to obtain another fact:
[2.23] (Transitive property of being a multiple*)
If a first natural number is a multiple of a second natural number, and that second natural number is a multiple of a third natural number, then the first natural number is a multiple of the third.
The dual of "No divisor of a natural number is greater than that natural number" is "No multiple of a natural number is less than that natural number." The duals of some true statements are false. One must be careful in forming dual statements of true statements. The dual of "each natural number has a finite number of divisors" is "each natural number has an infinite number of multiples." A simple way to get all the multiples of any natural number is to multiple all the natural numbers by that number.
A multiple is common to two or more lists of multiples if it is in all the lists.
The list of all multiples of 4 is {4,8,12,16,20,24,28,32,36,40, ...}
The list of all multiples of 6 is {6,12,18,24,30,36,42, ...}
The list of all common multiples of 4 and 6 is {12,24,36,... }
[2.24] (Least Common Multiple*)
The least common multiple of two natural numbers is the smallest multiple that is in both lists of all multiples.
Notation: lcm(m,n) = least common multiple of natural numbers m and n.
Click here for a technical definition of lcm.
Example: in the list of all common multiples of 4 and 6, 12 is the smallest. So lcm(4,6) = 12.
Comparing the definition [2.24] of lcm with the definition [2.19] of gcd, it is obvious that the definitions are duals of each other.
Recall the addition of fractions. To add two fractions it is necessary to have the same denominators. The numerator and denominator of each fraction can be multiplied by the same factor to make denominators equal. Therefore, the denominators must be a common multiple of the original denominators.

In the adjoining figure, 4 and 6 are the original denominators. Their product 24 is a common multiple. Multiply the numerator and denominator of the first fraction by 6 and multiply the numerator and denominator of the second fraction by 4 to get new fractions 18/24 and 4/24. These fractions are equivalent to the original 3/4 and 1/6, and can be added to get 22/24. Reduced to lowest terms the final fraction is 11/12.
In the second row of the figure the hcf(4,6) =12 is used as the common denominator. Less computation is needed there.
***
There is a connection between gcd and lcm:
[2.25] (*)
The product of thegcd and lcm of any pair of natural numbers is equal to their simple product.
Notation: for any pair of natural numbers m,n, gcd(m,n) x lcm(m,n) = m x n.
Example: Since gcd(4,6) = 2; and lcm(4,6) = 12 then 2 x 12 = 4 x 6.
There is no algorithm supplied here to find directly the lcm of two natural numbers m,n. The lcm(m,n) can be found by computing the gcd(m,n) and then evaluating the quotient in lcm(m,n) = mn/gcd(m,n). In short: lcm = product/gcd.
Example: lcm (8,20) = 8 x 20/gcd(8,20) = 160/4 = 40.
In this example the product of 8 and 20 is computed before the division by the gcd(8,20)=4. Smaller numbers will be used if the gcd is divided into the larger of the two given numbers numbers, which is 20, to produce 5. Then multiply the 8 by 5 to get the lcm:
lcm(8,20) = 8 x 20/gcd(8,20) = 8 x 20/4 = 8 x 5 = 40. This procedure of division before multiplication may avoid some large numbers.
The proof of [2.25] uses the technical definitions of gcd and lcm and a repeat use of logical implication. Click here to see those definitions and the proof. Another proof uses the complete factorization of any natural number (except 1) into powers of primes. Click here for a discussion of complete factorization. Click here to see a discussion supporting [2.25] using the complete factorization.
***
The the following "lemmas" are actually theorems of lesser importrance, except that they will be used in the the discussion on integers and non-negative integers. For their proofs click here.
[2.26] (Lemma)
If the product of two natural numbers is 1 then each of those natural numbers equals 1.
Notation: If mn = 1 then m = n = 1.
An indirect proof can be used here. Suppose n>1. Then m + m + ... +m =1, where m appears n times. But for natural numbers, the sum is greater than any of its parts. This means that 1 > m which is impossible for natural numbers. So n = 1. A similar argument exists for nm = 1.
[2.27] (Lemma*)
If two natural numbers are divisors of each other, then those numbers are equal.
Notation: If m | n and n | m then m = n.
If m | n then for some natural number x, n = mx. if n | m then for some natural number y, m = ny. Replace m in the equation n = mx by ny to get n = nyx. It will be shown in the next chapter that it is possible to divide both sides by n to get 1 = yx. By [2.26] x = y = 1. Replacing y in the equation m = ny by 1 produces m = n.
 This principle allows the natural numbers to be assigned to consecutive points (markers) on a horizontal straight line, starting with 1 and going to the right. By this assignment a smaller number is located to the left of a larger number. A larger number is located to the right of a smaller number. But those readers who are familiar with complex numbers have seen a system in which some numbers cannot be compared for size: it cannot be said which of the numbers 3 + 4i and 4 + 3i is larger than the other. The points for all complex numbers is a plane, not a line. The complex numbers are not linearly ordered. Complex numbers form a number system that discussed in chapter 5 in this same volume of number systems.
This principle allows the natural numbers to be assigned to consecutive points (markers) on a horizontal straight line, starting with 1 and going to the right. By this assignment a smaller number is located to the left of a larger number. A larger number is located to the right of a smaller number. But those readers who are familiar with complex numbers have seen a system in which some numbers cannot be compared for size: it cannot be said which of the numbers 3 + 4i and 4 + 3i is larger than the other. The points for all complex numbers is a plane, not a line. The complex numbers are not linearly ordered. Complex numbers form a number system that discussed in chapter 5 in this same volume of number systems.
 Finding areas of rectangles by multiplying lengths of adjacent sides suggests a more organized method for evaluating a product of natural numbers. Let the objects being counted small squares. Instead of using repeated addition (linear form) sq sq sq sq + sq sq sq sq + sq sq sq sq and then counting the sq's, use a two-dimensional rectangular form wiith rows of 4 squares under each other, as shown in the adjacent figure, and then count the squares. This suggests that areas of geometric rectangles provide a method to calculate the product of two natural numbers.
Finding areas of rectangles by multiplying lengths of adjacent sides suggests a more organized method for evaluating a product of natural numbers. Let the objects being counted small squares. Instead of using repeated addition (linear form) sq sq sq sq + sq sq sq sq + sq sq sq sq and then counting the sq's, use a two-dimensional rectangular form wiith rows of 4 squares under each other, as shown in the adjacent figure, and then count the squares. This suggests that areas of geometric rectangles provide a method to calculate the product of two natural numbers.
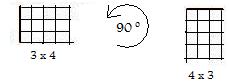 Mathematical induction can be used to prove this law for natural numbers. However, a simple geometric argument supports it. Draw the rectangle with height m and width n. Then there are mn squares inside the rectangle. Rotate the triangle through 90° Now it is a nm rectangle. The number of squares is the same because the two rectangles are congruent. The figure to the right shows this argument for the product 3x4 = 4x3.
Mathematical induction can be used to prove this law for natural numbers. However, a simple geometric argument supports it. Draw the rectangle with height m and width n. Then there are mn squares inside the rectangle. Rotate the triangle through 90° Now it is a nm rectangle. The number of squares is the same because the two rectangles are congruent. The figure to the right shows this argument for the product 3x4 = 4x3.