Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Return to index of all chapters in this volume
Volume B Chapter 5
The Complex Numbers
Section 1: Basics of Complex Numbers
In solving daily problems, numbers often are involved. The numbers are in systems that allow the solution of some numerical problems. Some systems are intuitively too "small" to solve many other problems, and need to be "expanded."
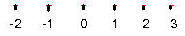 The positive integers 1,2,3,... can be used to express the number of whole objects are being considered: 5 automobiles, 4 tires, a dozen eggs. Using negative integers, zero and positive integers, the transfer of money can be indicated: + 7 dollars will mean that I receive the money (my wealth increases), -7 dollars means that I surrender the money and give it to someone else (my wealth decreases). 0 dollars mean no money is transferred (the status of my wealth has not changed). The system of integers appears as equally spaced collinear points on the invisible number line. Often the letters m and n denote integers in these discussions.
The positive integers 1,2,3,... can be used to express the number of whole objects are being considered: 5 automobiles, 4 tires, a dozen eggs. Using negative integers, zero and positive integers, the transfer of money can be indicated: + 7 dollars will mean that I receive the money (my wealth increases), -7 dollars means that I surrender the money and give it to someone else (my wealth decreases). 0 dollars mean no money is transferred (the status of my wealth has not changed). The system of integers appears as equally spaced collinear points on the invisible number line. Often the letters m and n denote integers in these discussions.
 The system of integers is not "big" enough to provide numerical solutions to other problems. The solution to the problem of separating 7 pounds of salt into two equal parts, say to give to two people, requires fractions. The fraction 7/2 = 3 + (1/2) shows the amount of salt in each part.. If I receive the portion of the salt then +7/2 indicates the transaction. But if I must give up the portion of the salt and give to someone else then -7/2 indicates the direction of the transaction. All the positive fractions, negative fractions and zero make up the system of rational numbers. The integers are included among the fractions because any integer can be written as a fraction with a 1 as denominator: n = n/1. This system of fractions appears on the number line as "filling in" like ground up light blue salt the spaces between the integers.
The system of integers is not "big" enough to provide numerical solutions to other problems. The solution to the problem of separating 7 pounds of salt into two equal parts, say to give to two people, requires fractions. The fraction 7/2 = 3 + (1/2) shows the amount of salt in each part.. If I receive the portion of the salt then +7/2 indicates the transaction. But if I must give up the portion of the salt and give to someone else then -7/2 indicates the direction of the transaction. All the positive fractions, negative fractions and zero make up the system of rational numbers. The integers are included among the fractions because any integer can be written as a fraction with a 1 as denominator: n = n/1. This system of fractions appears on the number line as "filling in" like ground up light blue salt the spaces between the integers.
 Even though the system of rational numbers satify the needs of simple business problems it does not fill up solidly the number line completely. The equation x² = 2 cannot be solved using fractions. It can be shown that the square root of 2 is not rational. (Click here to see the proof.) Yet it corresponds to a point on the number line, somewhere between the fractions 1414/1000 and 1415/1000. It is possible to construct a line segment whose length is the square root of 2: a right triangle whose legs have length 1. Π is another point on the number line, not covered by any of the rational number points. There infinitely many tiny gaps (one point wide) in the light blue line above. The system of real numbers includes all rational numbers and all irrational numbers. The system fills the dark blue line completely. Often the letters a,b,c,d at the beginning of the alphabet denote real numbers. The letters x and y also denote real numbers. The other letters z,w,v,u denote numbers in a new system that is being developed now.
Even though the system of rational numbers satify the needs of simple business problems it does not fill up solidly the number line completely. The equation x² = 2 cannot be solved using fractions. It can be shown that the square root of 2 is not rational. (Click here to see the proof.) Yet it corresponds to a point on the number line, somewhere between the fractions 1414/1000 and 1415/1000. It is possible to construct a line segment whose length is the square root of 2: a right triangle whose legs have length 1. Π is another point on the number line, not covered by any of the rational number points. There infinitely many tiny gaps (one point wide) in the light blue line above. The system of real numbers includes all rational numbers and all irrational numbers. The system fills the dark blue line completely. Often the letters a,b,c,d at the beginning of the alphabet denote real numbers. The letters x and y also denote real numbers. The other letters z,w,v,u denote numbers in a new system that is being developed now.
The development of the real number system from the rational number system is beyond the scope of this section. One development uses the limits of convergent sequences of rational numbers to arrive at the completed real number system.
There are two ideas, absolute value and square root, that will be needed in future discussions.
The absolute value |x| of a real number x is a real number that is never negative. More precisely,
|x| = x if x positive or zero. |x| = -x if x is negative.
In this last situation -x is not negative because a double negative is always positive. |-2| = -- 2 = 2. |+3| = |3| = 3.
For a geometric interpretation, on the real number line the absolute value of any number is the (non-negative) distance between the origin and that number
The idea of a square root of a real number should already be familiar. If some number times itself = x then that number is the square root of x. For example, 3 and -3 are square roots of 9 because 3x3=9 and (-3)x(-3) = 9.Every positive real number has two distinct roots. The square roots of negative numbers will be discussed below.
Every square root of a positive real number has a positive real root. The common notation for a square root might not be produced on some screens and printers in future discussions. The symbol sqrt is often used in some computer programming languages. By definition
sqrt(x) = the positive square root of x. Also sqrt(0) = 0.
sqrt(16) = 4. sqrt(25) = 5. sqrt(2) = 1.414....
A curious connection between absolute value and square root is
|x| = sqrt(x²).
A full number line gives the impression that the real number system is the ultimate number system. Yet it does not supply an answer to what is sqrt(-1)? There is no real number times itself = -1. No solution for x² = -1. The answer lies outside the real number system. A larger number system is needed.
 As a starting point
As a starting point
[1.1] A special "number" i is invented to solve the problem of a square root of -1:
i² = -1.
It is called an imaginary number, because it cannot be real. Whatever it is, i has a constant value, never changing. Intuitiviely, i + i = 2i. Similarly for 3i, 4i, 1i = i... .
There exists -i, -2i, -3i,.... . (1/2)i, (-9/5)i, sqrt(5)i. In general, yi is called an imaginary number, where y is a real number. Zero is the only number both real and imaginary: 0 = 0i.
These imaginary numbers (except 0) cannot be on the real line (no room for any of them). Another line is created to contain them as equally spaced points. This line, called the imaginary axis in perpendicular to the real number axis. It contains all numbers of the form yi. They fill up the imaginary axis completely. The two axes intersect at 0 and determine a plane called the complex plane.
[1.2] In general the new numbers have the standard form x + yi where x and y are real numbers. The real part is x and the imaginary part is yi. Either x or y may be zero and a part need not be written, but it still exists. The coefficients are x and y. A number with a real part and an imaginary part is called a complex number. They are also called imaginary even if real part is not zero.
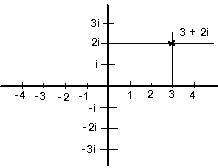
At the intersection of the two lines the complex number 0 is equal to 0 + 0i. The complex number 3 + 2i is located in the figure of the complex plane.
Often it is more convenient to use a single single symbol to denote a complex number. The letters z,w,u,v are used for this purpose. They can be given complex number values:
(*) z = 3 + 2i, w = 4 - i, u = i, v = 6
Note that the real part and the imaginary part of a single complex number in standard form cannot be combined under addition or subtraction (nor multiplication nor division to be discussed soon), but must be left in tact. The existance of i forces this separation of the real and imaginary parts.
[1.3] The system of real numbers is a part of the system of complex numbers because in the complex number x + yi the coefficient y may be zero: x = x + 0i. Also the horizontal real axis is embeded in the complex plane.
[1.4] The equality of two complex numbers produces two equations involving real numbers. If z = a + bi and w = c + di then z = w if and only if a = c and b = d.
In other words, two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. For more discussion of this fact click here.
The addition of two complex numbers z = a + bi and w = c + di is intuitively clear: simply add like terms, add the real parts and add the imaginary parts:
z + w(a + bi) + (c + di) = (a + c) + (b + d)i.
The multiplication of a real number and a complex number is also obvious:
aw = a(c + di) = ac + adi.
From elementary algebra the product:
(**)(U + V)(X + Y) = UX +UY + VX + VY
The multiplication zw of two complex numbers z = a + bi and w = c + di is done in a similar way
zw = (a + bi)(c + di) = ac + (ad + bc)i + bdi².
But the expression on the right side of the equation is not in the standard form of a complex number, not until i² is somehow assigned permanently a value. The value will be -1:
i² = -1.
One reason for the choice of -1 is that i is a solution to the equation
z² = -1.
Then -4, -9, -16 have as square roots the pairs: 2i and -2i, 3i and -3i, 4i and -4i respectively.
For more discussions supporting the choice of -1 to be the permanent value of i² click here.
[1.5] The product of two complex numbers in standard form can now be carried out to give a product in standard form:
(3 + 4i)(2 + 5i) = 6 + 15i + 8i + 20i² = 6 + 23i - 20 = -14 + 23i.
To multiply two complex numbers, follow the pattern (**) and replace i² by -1.
Before the operation of division of complex numbers is discussed, it it convenient to introduce a simple definition that will simplify the process of division.
[1.6] The conjugate of any complex number x + y i is the complex number x - y i.
In other words, the conjugate of a complex number is obtained by negating the imaginary part.
The conjugates of
3 + 2i, 4 - i, i, 6 are respectively 3 - 2i, 4 + i, -i, 6
 It is convenient to use sometimes the single symbol for a complex number and its conjugate. If z is a complex number then its conjugate in this work is denoted by z*. The usual bar notation for a conjugate, shown in the adjacent figure, is not available on all browsers.
It is convenient to use sometimes the single symbol for a complex number and its conjugate. If z is a complex number then its conjugate in this work is denoted by z*. The usual bar notation for a conjugate, shown in the adjacent figure, is not available on all browsers.
For more properties of conjugation not discussed below see the exercises by clicking here.
Using the identity (U + V)(U - V) = U² - V², it is easy to prove that the product of any complex number and its conjugate is always a real number: zz* = a real number. This fact is useful in performing a division operation.
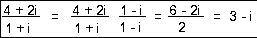 (4 + 2i)/(1 + i) is a typical division problem where 4 + 2i is divided by 1 + i. If the denominator 1 + i is multiplied by its conjugate 1 - i the product is the real number 2. Therefore, multiply both numerator 4 + 2i and denominator 1 + i by that conjugate 1 - i to get the fraction (6 - 2i)/2 = 3 - i. The figure to the right shows this division operation in more standard notation.
(4 + 2i)/(1 + i) is a typical division problem where 4 + 2i is divided by 1 + i. If the denominator 1 + i is multiplied by its conjugate 1 - i the product is the real number 2. Therefore, multiply both numerator 4 + 2i and denominator 1 + i by that conjugate 1 - i to get the fraction (6 - 2i)/2 = 3 - i. The figure to the right shows this division operation in more standard notation.
[1.7] In general, to perform the division z/w of two complex numbers z and w multiply both numerator z and denominator w by the conjugate of the denominator w: zw*/ww*. Then divide the real number denominator into the numerator.
For practice doing division of complex numbers click here
Section 2: The unit circle
In the appendix (click *****) another unit circle is discussed and is located in the ordinary xy-coordinate plane. Here the unit circle is part of the complex plane. Some important trigonometric relations can be deerived more easily using this unit circle.
Setwise the unit circle here is a subset of the complex numbers. Geometrically its center is at the origin where the real and imaginary axes intersect. It has a radius of 1. Algebraicly a complex number is on this circle if and only if the absolute value = 1. This circle has interesting yet simple properties: algebraic, geometric and trigonometric to be discussed in this chapter.
Examples of unit complex numbers: i, -1, (1 + i)/21/2, where 21/2 is the square root of 2
[2.1] (Normalizing a non-zero complex number) Except for zero, any complex number z can be converted to a unit complex number by dividing it by its absolute value.
Notation: z/|z| has length 1
This quotient equals 1 because its absolute value = |z|/|z| = 1.
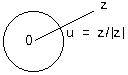
Let u = z/|z| be the unit complex number. Geometrically u is obtained by sliding the point along half-line 0z onto the point, where the line segment 0z intersects the circle. See adjacent figure.
Intuitively speaking, the unit vector indicates a direction. Two complex numbers have the same direction if their unit vectors coincide. Similar statements exist for opposite directions, at right angles,... etc.
Because of theorem [1.5] the following is true:
[2.2] (The product of unit complex numbers) The product of unit complex numbers is a unit complex number.
Notation: if z and w have length 1 then zw has length 1
This is true because for the lengths involved (1)(1) = 1.
[2.3] (Quotient of unit complex numbers) The quotient of two unit complex numbers is a unit complex number.
Notation: if z and w have length 1 then z/w has length 1
This is true because for the lengths involved (1)/(1) = 1.
This is enough to guarantee that the unit circle is a multiplicative subgroup of the multiplicative system of complex numbers, a term used in modern algebra.
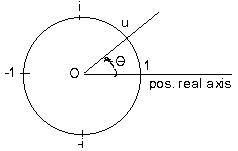 In the adjoining figure is a unit circle with a point u, a unit complex number on it. Also in the figure is part of the positive real number axis where 1 is the intersection of the unit circle and the positive real axis. An angle θ can be measured from that axis to the line through O and u. If θ is measured in the counter-clockwise direction then θ is positive. (If in the clockwise direction, then θ is negative.)
In the adjoining figure is a unit circle with a point u, a unit complex number on it. Also in the figure is part of the positive real number axis where 1 is the intersection of the unit circle and the positive real axis. An angle θ can be measured from that axis to the line through O and u. If θ is measured in the counter-clockwise direction then θ is positive. (If in the clockwise direction, then θ is negative.)
The central angle θ needs to have measurement. A natural measure of the angle is to compare the arc from 1 to u to the entire circumference of the circle. For example, in the figure θ appears to be about 1/8 of the entire circle. Therefore θ = 1/8 rev. If u moves to the top of the circle (u = i) then θ = 1/4 rev = right angle. If θ = 1/2 then u = -1 and θ is a straight angle. If u starts at 1 and goes around the entire circle three times then θ = 3 rev. The system of measuring in revolutions is useful for indicating speed of an engine, so many revolutions per minute.
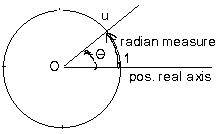 Another "natural" measurement of angles is the radian., which is useful in the mathematical subject of calculus. The number of radians in θ is the comparision of length of arc from 1 to u to the length of the entire circle. But the entire circumference has length 2π. For a straight angle (u = -1) the angle θ = π. For a right angle (u = i), θ = π/2.
Another "natural" measurement of angles is the radian., which is useful in the mathematical subject of calculus. The number of radians in θ is the comparision of length of arc from 1 to u to the length of the entire circle. But the entire circumference has length 2π. For a straight angle (u = -1) the angle θ = π. For a right angle (u = i), θ = π/2.
The most common measurement of an angle is with degrees. The number of degrees in 1 revolution has been defined as 360. (Perhaps related to the number 365 days in a year.) If θ is a right angle then &theta = 90°. For a straight angle, θ = 180°. Click here for a more detailed discussion of angles and the various measurements of them
Starting from the positive real axis the central angle θ completely and uniquely determines the half-line 0u, and hence the unit complex number u. The equation u = cis θ expresses this relationship. (The abbreviation cis will be explained later.) Do not confuse cis with cos, which is a common trigonometric function.
Examples: cis 0 = 1, cis 90° = i, cis -90° = -i, cis π = -1, cis 3π/2 = -i, cis (2 rev) = 1, cis 1350° = -i.
The last equality is true because -i = cis 270° and 270 + 3 revolutions = 270 + 3(360) = 1350.
In general cis θ = cis φ if θ - φ = some number of whole revolutions. Click here for a discussion of angles and the various measurements of them.
As mentioned above, any non-zero complex number z can be normalizied and written in the form z = |z| u where u is a point on the unit circle. This unit complex number u = cis θ for some central angle θ. Therefore, z can be written in a polar form: z = r cis θ where r is a real number and r = |z| .
For a short discussion of another expression eiθ that is also a unit vector equal to cis θ, click here
The product of unit complex numbers has an interesting relationship with the angles that they make with the positive real axis:
[2.4] (de Moivre's theorem) For any angles (real numbers) θ and φ,
cis(θ + φ) = (cis θ)(cis φ).
Intuitively speaking cis converts a sum of angles into a product of cis's of those angles. This sounds similar to the law of exponents: ez+w = ezew. Assuming the relation cis ω = eiω:
cis (θ+φ) = eiθ+iφ = eiθeiφ = (cis θ)(cis φ).
This is not a genuine proof of the theorem, because the number e has not been defined and the relation eiω = cis ω has not been proven. (The proof of that relation involving a complex number as exponent is beyond the scope of these notes.) However, click here to see a geometric proof that does not involve the number e.
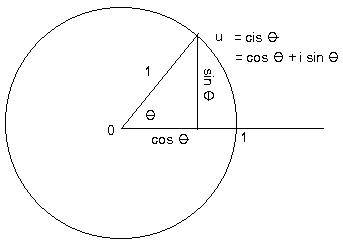 The function cis θ allows the definition of two basic trigonometric functions sine and cosine The functions sin θ and cos θ are defined here as the coefficients of the imaginary and real parts of cis θ:
The function cis θ allows the definition of two basic trigonometric functions sine and cosine The functions sin θ and cos θ are defined here as the coefficients of the imaginary and real parts of cis θ:
cis θ = cos θ + i sin θ
This identity explains the abbreviation cis.
But cis θ is a unit complex number. Then the sum of the squares of its real and imaginary coefficients must equal 1. The identity cos² θ + sin² θ = 1 is a well known trigonometric identity.
The familiar trigonometric identities
(#) cos(θ + φ) = cos θ cos φ - sin θ sin φ
(##) sin(θ + φ) = sin θ cos φ + cos θ sin φ
can be proven using the DeMoivre theorem:
($) cos(θ + φ) + i sin(θ + φ) =
cis(θ + φ) = [DeMoivre's theorem used here]
(cis θ)(cis φ) =
(cos θ + i sin θ)(cos φ + i sin φ) =
($$) (cos θ cos φ - sin θ sin φ) + i (sin θ cos φ + cos θ sin φ).
Equating the coefficients of the real parts of ($) and ($$) gives (#). Equating the coefficients of the imaginary parts of ($) and ($$) gives (##).
 The positive integers 1,2,3,... can be used to express the number of whole objects are being considered: 5 automobiles, 4 tires, a dozen eggs. Using negative integers, zero and positive integers, the transfer of money can be indicated: + 7 dollars will mean that I receive the money (my wealth increases), -7 dollars means that I surrender the money and give it to someone else (my wealth decreases). 0 dollars mean no money is transferred (the status of my wealth has not changed). The system of integers appears as equally spaced collinear points on the invisible number line. Often the letters m and n denote integers in these discussions.
The positive integers 1,2,3,... can be used to express the number of whole objects are being considered: 5 automobiles, 4 tires, a dozen eggs. Using negative integers, zero and positive integers, the transfer of money can be indicated: + 7 dollars will mean that I receive the money (my wealth increases), -7 dollars means that I surrender the money and give it to someone else (my wealth decreases). 0 dollars mean no money is transferred (the status of my wealth has not changed). The system of integers appears as equally spaced collinear points on the invisible number line. Often the letters m and n denote integers in these discussions.
 The system of integers is not "big" enough to provide numerical solutions to other problems. The solution to the problem of separating 7 pounds of salt into two equal parts, say to give to two people, requires fractions. The fraction 7/2 = 3 + (1/2) shows the amount of salt in each part.. If I receive the portion of the salt then +7/2 indicates the transaction. But if I must give up the portion of the salt and give to someone else then -7/2 indicates the direction of the transaction. All the positive fractions, negative fractions and zero make up the system of rational numbers. The integers are included among the fractions because any integer can be written as a fraction with a 1 as denominator: n = n/1. This system of fractions appears on the number line as "filling in" like ground up light blue salt the spaces between the integers.
The system of integers is not "big" enough to provide numerical solutions to other problems. The solution to the problem of separating 7 pounds of salt into two equal parts, say to give to two people, requires fractions. The fraction 7/2 = 3 + (1/2) shows the amount of salt in each part.. If I receive the portion of the salt then +7/2 indicates the transaction. But if I must give up the portion of the salt and give to someone else then -7/2 indicates the direction of the transaction. All the positive fractions, negative fractions and zero make up the system of rational numbers. The integers are included among the fractions because any integer can be written as a fraction with a 1 as denominator: n = n/1. This system of fractions appears on the number line as "filling in" like ground up light blue salt the spaces between the integers.
 Even though the system of rational numbers satify the needs of simple business problems it does not fill up solidly the number line completely. The equation x² = 2 cannot be solved using fractions. It can be shown that the square root of 2 is not rational. (Click
Even though the system of rational numbers satify the needs of simple business problems it does not fill up solidly the number line completely. The equation x² = 2 cannot be solved using fractions. It can be shown that the square root of 2 is not rational. (Click  As a starting point
As a starting point
 It is convenient to use sometimes the single symbol for a complex number and its conjugate. If z is a complex number then its conjugate in this work is denoted by z*. The usual bar notation for a conjugate, shown in the adjacent figure, is not available on all browsers.
It is convenient to use sometimes the single symbol for a complex number and its conjugate. If z is a complex number then its conjugate in this work is denoted by z*. The usual bar notation for a conjugate, shown in the adjacent figure, is not available on all browsers.
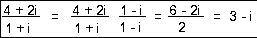 (4 + 2i)/(1 + i) is a typical division problem where 4 + 2i is divided by 1 + i. If the denominator 1 + i is multiplied by its conjugate 1 - i the product is the real number 2. Therefore, multiply both numerator 4 + 2i and denominator 1 + i by that conjugate 1 - i to get the fraction (6 - 2i)/2 = 3 - i. The figure to the right shows this division operation in more standard notation.
(4 + 2i)/(1 + i) is a typical division problem where 4 + 2i is divided by 1 + i. If the denominator 1 + i is multiplied by its conjugate 1 - i the product is the real number 2. Therefore, multiply both numerator 4 + 2i and denominator 1 + i by that conjugate 1 - i to get the fraction (6 - 2i)/2 = 3 - i. The figure to the right shows this division operation in more standard notation.
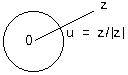
 In the adjoining figure is a unit circle with a point u, a unit complex number on it. Also in the figure is part of the positive real number axis where 1 is the intersection of the unit circle and the positive real axis. An angle θ can be measured from that axis to the line through O and u. If θ is measured in the counter-clockwise direction then θ is positive. (If in the clockwise direction, then θ is negative.)
In the adjoining figure is a unit circle with a point u, a unit complex number on it. Also in the figure is part of the positive real number axis where 1 is the intersection of the unit circle and the positive real axis. An angle θ can be measured from that axis to the line through O and u. If θ is measured in the counter-clockwise direction then θ is positive. (If in the clockwise direction, then θ is negative.)
 Another "natural" measurement of angles is the radian., which is useful in the mathematical subject of calculus. The number of radians in θ is the comparision of length of arc from 1 to u to the length of the entire circle. But the entire circumference has length 2π. For a straight angle (u = -1) the angle θ = π. For a right angle (u = i), θ = π/2.
Another "natural" measurement of angles is the radian., which is useful in the mathematical subject of calculus. The number of radians in θ is the comparision of length of arc from 1 to u to the length of the entire circle. But the entire circumference has length 2π. For a straight angle (u = -1) the angle θ = π. For a right angle (u = i), θ = π/2.
 The function cis θ allows the definition of two basic trigonometric functions sine and cosine The functions sin θ and cos θ are defined here as the coefficients of the imaginary and real parts of cis θ:
The function cis θ allows the definition of two basic trigonometric functions sine and cosine The functions sin θ and cos θ are defined here as the coefficients of the imaginary and real parts of cis θ: