Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Return to index of all chapters in this volume
Volume B Chapter 6
Quaternions
Section 1: Expanding number systems
There are two reasons for discussing the number system called quaternions. The first reason is to attempt a "natural" expansion of the scope of mathematical ideas that have been discussed. A significant expansion was discussed in Chapter 5 of this volume. The complex numbers came from the real numbers by inventing an imaginary number i and forming the general complex number a + bi, where a and b were real numbers. The usual operations of addition, subtraction, multiplication and division along with some important laws (distributive, associative and other laws) of the real numbers were carried over to complex numbers. Can the complex numbers be expanded to create a "bigger" number system with the usual operations and laws? It will turn out that one of the laws is not included in the system of quaternions.
In the systems of real and complex numbers the product of two numbers is the same no matter in what order the multiplcation is done: ab = ba, zw = wz. The numbers a,b and z,w are said to commute. If all pairs of numbers commute then the system is called commutative, or said to obey the commutative law. Very shortly it will be evident that multiplication of quaternions are not commutative. This is the second reason for discussing quaternions: to introduce a non-commutative number system. Some readers may already be familiar with matrix multiplication which is not commutative. But matrices are not usually considered as being a number system.
A first natural attempt at generalizing the complex number system may be to invent a new "super" number j which does not exist in the complex numbers but is a super unit number. A complex number should be part of the new number system and then include j to get the general form of a super number: a + bi + cj. To the 2-dimensional complex plane, another axis, the j axis, is constructed through the origin, and perpendicular to the complex plane. The super numbers fill up all of 3-dimensional space. A super number has an absolute value, namely |a + bi + cj| = ( a² + b² + c²)1/2. But using mathematics beyond the scope of this text, it can be shown that a number system, with the usual four fundamental operations of arithmetic and the usual laws for those operations, cannot be made out of 3-dimensional space.
Another approach can be tried. Notice the form a + bi is made using real coefficients a,b. Now construct a new form with complex numbers as coefficients and with j given above:
q = z + wj where z and w are complex numbers.
Let z = a + b i and w = c + d i, where a,b,c,d are real numbers. Then
q = z + w j = (a + b i) + (c + d i)j = a + b i + c j + d ij.
The product ij cannot be back in 3-dimensional space, since those super numbers cannot have all the usual operations and laws. A new number k is invented to equal this product. Therefore k is outside three dimensional space. Since the absolute values |k| = |ij| = |i||j| = (1)(1) = 1, k must be a unit number. (More discussion of absolute value of a quaternion is discussed in Section 2.)
[1.1] (Form of a quaternion) The standard form of a quaternion is
a + b i + c j + d k,
where i,j,k are unit quaternions and the coefficients a,b,c,d are real numbers.
Examples:
1 + 2 i + 3 j + 4 k, -5 + 3 i + 2j - 6 k, i - k, - j
A quaternion may be denoted by a single letter, often q:
q = a + b i + c j + d k
Quaternions are denoted by letters in bold face but real numbers as coefficients are not in bold face. This presents a slight problem with real numbers. Since a = a + 0 i + 0 j + 0 k a real number may be considered a quaternion. As a quatrnion it is presented in bold face and as a real number coefficient it is not. In particular 0 and 1 are quaternions, while 0 and 1 are real numbers.
A complex number
z = a + bi
may be written as an ordered pair:
z = (a,b)
Similarly, the quaternion q above may be written as a 4-tuple:
q = (a,b,c,d)
This short notation gives quaternions an abstract geometric interpretation, namely, a point in a hyperspace of dimension 4. But more important here it is useful to indicate imput of quaternions into accompanying computer programs. Even some simple operations such as multiplication and division often involves much arithmetical computation.
.
Section 2: Basics of Quaternions
Again using the model of the complex number z = a + bi, the absolute value is
|z| = (a2 + b2)1/2
The following definition extends absolute value to quaternions:
[2.1] (Absolute value of a quaternion) The absolute value of a quaternion (in standard form) is the square root of the sum of the squares of all four coefficients.
Notation: if q = a + b i + c j + d k then
|q| = (a2 + b2 + c2 + d2)1/2.
The absolute value is always a real number that is never negative.
Examples:
if q = 3 + 4i then |q| = (9 + 16)1/2 = 5.
if q = 2 + 4i + 4j + 8k then |q| = (4 + 16 + 16 + 64)1/2 = 10
then |q| = -2 + 2i - 6j + 10k then |q| = (4 + 4 + 36 + 100)1/2 = 12
|(1,1,3,5)| = 6
|(1046,1057,1094,1100)| = 2149 (time to let the computer do this one!)
The absolute value of i is |i| = (02 + 12 + 02 + 02)1/2 = 1.
Similarly, |j| = 1 and |k| = 1
[2.2] (Zero absolute value) The absolute value of a quaternion is zero if and only if all four of its real number coefficients are zero.
Notation: |(a,b,c,d)| = 0 if and only if a=0 and b=0 and c=0 and d=0.
This is a result of a statement about real numbers: the sum of squares of real numbers is zero if and only if each of those real numbers is zero.
Quite often two quaternions are involved in the same discussion.
If q1 = a1 + b1 i + c1 j + d1 k
and
q2 = a2 + b2 i + c2 j + d2 k
then the corresponding coefficients of q1 and q2 are the pairs of real numbers
a1,a2, b1,b2, c1,c2, and d1,d2.
It is important to specify the conditions that two quaternions be equal.
[2.3] (Equality of quaternions) Two quaternions are equal if and only each of the coefficients of the first quaternion is equal to the corresponding coefficient of the second quaternion.
Notation:
a1 + b1 i + c1 j + d1 k = a2 + b2 i + c2 j + d2 k if and only if
a1 = a2, b1 = b2, c1 = c2, and d1 = d2
Four equations with real numbers are involved for the equality of two quaternions.
Recall that an imaginary number z = a + bi has a real part a and an imaginary part bi. A similar situation exists with quaternions. Each quaternion q = a + bi + cj + dk contains a real part a and a vector part v = bi + cj + dk. Therefore q = a + v. (See Volume D for more information about vectors.)
[2.4] (Conjugate of a quaternion) The conjugate of a quaternion is obtained by negating the last three coefficients.
Notation: The conjugate q = a + v is q^ = a - v.
It is easy to prove the following:
[2.5] (Equality of quaternions and conjugates) The absolute value of any quaternion is equal to the absolute value of its conjugate
Notation: |q| = |q^|.
Both are equal to (a2 + b2 + c2 + d2)1/2.
[2.6a] (Addition of quaternions) The sum of two quaternions is that quaternion whose coefficients are sums of corresponding coefficients of the two given quaternions.
Notation:
If q1 = a1 + b1 i + c1 j + d1 k
and
q2 = a2 + b2 i + c2 j + d2 k
then q1 + q2 = (a1 + a2) + (b1 + b2)i + (c1 + c2)j + (d1 + d2)k
[2.6b] (Subtraction of quaternions) The difference of two quaternions is that quaternion whose coefficients are differences of corresponding coefficients of the two given quaternions.
Notation:
If q1 = a1 + b1 i + c1 j + d1 k
and
q2 = a2 + b2 i + c2 j + d2 k
then q1 - q2 = (a1 - a2) + (b1 - b2)i + (c1 - c2)j + (d1 - d2)k
If q = a + b i + c j + d k then -q = -a - b i - c j - d k. Simply take q1 = 0 and q2 = q.
Multiplication of quaternions depend upon the products of the unit quaternions i,j,k. They are defined as follows:
ij = k, jk = i, ki = j, and kj = - i, ik = - j, ji = - k.
 [2.7] (Products of the unit quaternions) The product of any two of the unit quaternions i,j,k is as follows:
[2.7] (Products of the unit quaternions) The product of any two of the unit quaternions i,j,k is as follows:
(a) The product is equal to the remaining unit quaternion if the product is taken in counter-clockwise order in the adjacent figure.
(b) The product is equal to the negative of the remaining unit quaternion if the product is taken in clockwise order in the adjacent figure.
The following table contains all possible products of i,j,k:
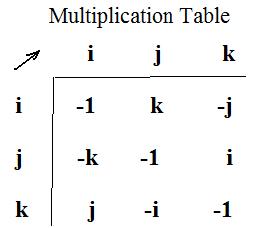 The left column contains the first unit quaternion of a product, the top row contains the second.
The left column contains the first unit quaternion of a product, the top row contains the second.
Usually computing the product of two quaternions ( a + bi + cj + dk)( e + fi + gj + hk) involves many arithmetical operations. A computer program can be written to do these operations and give the product in standard quaternion form.
To see one such program click here.
It is not difficult to show that the product of the vector v with itself is: vv = -b² - c² - d². Therefore, qq* = (a + v)(a - v) = a² - vv = a² + b² + c² + d². Therefore:
[5] The product of any quaternion and its conjugate is equal to the square of its absolute value.:
qq* = a² + b² + c² + d² = |q|²
Note: the equality vv = -b² - c² - d² and hence qq* = |q|² would be false if the product ji = k and not -k as given above.
By definition ij = k and ji = -k. The products ji and ij are not equal. Hence i and j do not commute. The system of quaternions provides an example of a system of numbers which is not commutative. But there are some situations where pairs of quaternions do commute. A simple example is any product of a real number h (a real number is a quaternion with its vector part = 0) and any quaternion q:
hq = qh
because h commutes with each of the four coefficients of q : ha=ah, bh = hb, etc.
[6] Any real number and any quaternion commute.
Another important example is
[7] Any quaternion and its conjugate commute
Let q be any quaternion. This theorem states that
(q*)(q) = (q)(q*).
This equality follows from the identity
(a - v)(a + v) = (a + v)(a - v)
where both sides equal the square of the absolute value of q, namely |q|² and where the real number a commutes with the vector (quaternion) v.
A third example involves the (multiplicative) inverse of a quaternion not zero. (For an elementary introduction and discussion of inverses click here.) By [5] above, qq* = |q|². Then dividing both sides by the right side,
q(q*/ |q|²) = 1. This means that the inverse of q is q-1 = q*/ |q|². For clarity this same equality is given below in the boxed figure (a).
Using [7] above, it is easy to show that (q-1)(q) = 1. Therefore,
[8] Any non-zero quaternion and its inverse commute.
The above discussion supports the following theorem:
[9a] The inverse of any non-zero quaternion is obtained by dividing the conjugate by the square of the absolute value. (See figure (a) below.)
The inverse of q = j is q-1 = -j/|j|² = -j/1² | = -j. Check: (j)(- j) = - j² = 1
The inverse of q = 3 i + 4 k is
q-1 = (3 i - 4 k)/|3 i + 4 k|² = (3 i - 4 k)/25. (Let the reader provide the check: q(q-1) = 1.
For a reason given later, the reciprocal notation 1/q will not be used in these notes for the inverse q-1.
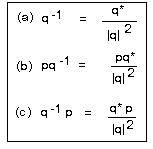 The above method for finding the inverse of a non-zero quaternion can be developed into performing division of quaternions. From elementary algebra the division of p by q is the same as multiplying p by the inverse q-1.
But by [9], q-1 = q*/ |q|². For clarity the next equation is given with fractions in the adjoining figure (b). But before we claim that (b) gives a method for finding the quotient, one must also consider (c). Very often p and q do not commute. Therefore, (b) and (c) may give different results. There may be two answers to p divided by q! Hence the fraction p/q is ambiguous because it does not indicate which computation (b) or (c) is used for finding the quotient.
The above method for finding the inverse of a non-zero quaternion can be developed into performing division of quaternions. From elementary algebra the division of p by q is the same as multiplying p by the inverse q-1.
But by [9], q-1 = q*/ |q|². For clarity the next equation is given with fractions in the adjoining figure (b). But before we claim that (b) gives a method for finding the quotient, one must also consider (c). Very often p and q do not commute. Therefore, (b) and (c) may give different results. There may be two answers to p divided by q! Hence the fraction p/q is ambiguous because it does not indicate which computation (b) or (c) is used for finding the quotient.
[9b] The right division (pq-1) of a quaternion by a non-zero quaternion is obtained by multiplying the first quaternion by the conjugate of the second quaternion, and dividing the result by the square of the absolute value of the second quaternion.
[9c] The left division (q-1p) of a quaternion by a non-zero quaternion is obtained by multiplying the conjugate of the second quaternion by the first quaternion, and dividing the result by the square of the absolute value of the second quaternion.
What do left and right divisions produce? Let quaternion r be the result of right division (b). Then pq-1 = r. Multiply both sides on the right by q to get the equation p = rq. So right division by q produces the answer before the factor q.
Let s be the result of left division (c). Then (q-1)(p) = s. Multiply both sides by q on the left to qet the equation p = qs. Therefore left division by q produces the answer after the factor q.
Click here to see the proof that the absolute value of the product of two quaternions is equal to the product of their individual absolute values:
|qr| = |q||r|.
The discussion above shows that quaternions enjoy most of the laws of complex numbers. The exception is the commutative law. For any two complex numbers z and w, zw = wz. But in general, there are many quaternions q and r such that qr is not equal to rq. The quaternions form a skew field.
It is impossible to impose an algebraic structure of a field or skew field on any dimension greater than 4. The Cayley numbers of dimension 8 have many of the algebraic laws that quaternions satisfy, except they are not associative.
 [2.7] (Products of the unit quaternions) The product of any two of the unit quaternions i,j,k is as follows:
[2.7] (Products of the unit quaternions) The product of any two of the unit quaternions i,j,k is as follows:
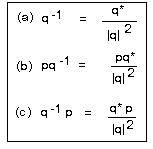 The above method for finding the inverse of a non-zero quaternion can be developed into performing division of quaternions. From elementary algebra the division of p by q is the same as multiplying p by the inverse q-1.
But by [9], q-1 = q*/ |q|². For clarity the next equation is given with fractions in the adjoining figure (b). But before we claim that (b) gives a method for finding the quotient, one must also consider (c). Very often p and q do not commute. Therefore, (b) and (c) may give different results. There may be two answers to p divided by q! Hence the fraction p/q is ambiguous because it does not indicate which computation (b) or (c) is used for finding the quotient.
The above method for finding the inverse of a non-zero quaternion can be developed into performing division of quaternions. From elementary algebra the division of p by q is the same as multiplying p by the inverse q-1.
But by [9], q-1 = q*/ |q|². For clarity the next equation is given with fractions in the adjoining figure (b). But before we claim that (b) gives a method for finding the quotient, one must also consider (c). Very often p and q do not commute. Therefore, (b) and (c) may give different results. There may be two answers to p divided by q! Hence the fraction p/q is ambiguous because it does not indicate which computation (b) or (c) is used for finding the quotient.